给定一个字符串，求最长回文子串(假设字符串中只有唯一的一个最长回文子串)。

注意子串和子序列的区别，子串是连续的，子序列是非连续的
例如：
字符串”xyzabccbad”, 最长回文为”abccba”
字符串”aaa”, 最长回文为”aaa”
字符串”bananas”, 最长回文为”anana”

回文就是顺着读和逆着读是一样的。

动态规划算法

最长回文子串可见是求最优解，并且可以对将此问题拆分，则观察能否用动态规划去尝试。

要用动态规划首先要找到转移方程，

这里需要注意，假如你发现自己的转移方程的特别繁琐或者需要考虑很多不同的情况更或者是总一些情况无法用转移方程表示时，这时你就应该考虑是否应该重新定义状态，进行重新整理转移方程。

假设：dp[i][j]表示i为开始j为结尾的字符串是否为回文，则转移方程如下：
dp[i][j] = true (chars[j] == chars[i] && dp[i+1][j-1])

初始条件是dp[i][i] = true (0<i<chars.length); dp[i][i+1] = chars[i] == charsi+1

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
public static String dp(String str){
    boolean[][] dp = new boolean[str.length()][str.length()];
    char[] chars = str.toCharArray();
    int longest = 0;
    int start = 0;
    StringBuffer stringBuffer = new StringBuffer();
    // 初始化dp数组，数组的值是当前子串是否为回文
    // 单个字符是回文，当chars[i] == chars[i+1]时，dp[i][i+1]的值为true
    for (int i=0; i<chars.length; i++){
        dp[i][i] = true;
        if ((i - i + 1) > longest){
            start = i;
            longest = i - i + 1;
        }
        if (i+1<chars.length && chars[i] == chars[i+1]){
            dp[i][i+1] = true;
            if (((i+1) - i + 1) > longest){
                start = i;
                longest = (i+1) - i + 1;
            }
        }else if (i+1 < chars.length){
            dp[i][i+1] = false;
        }
    }
    // k 是步长，k=1即i+1已初始化，则从2开始
    for (int k=2; k<chars.length; k++){
        int j = k;
        // i j组成一个二维数组(右上半角矩阵)，按照斜线向上填补矩阵
        for (int i=0; i<chars.length-k; i++){
        	// k从2开始的好处是当i=0，j=2时，dp[i+1][j-1]的值已被初始化
            if (chars[i] == chars[j] && dp[i+1][j-1]){
                dp[i][j] = true;
                if ((j - i + 1) > longest){
                    start = i;
                    longest = j - i + 1;
                }
            }else {
                dp[i][j] = false;
            }
            j++;
        }
    }

    for (int i=0; i<longest; i++){
        stringBuffer.append(chars[start+i]);
    }
    return stringBuffer.toString();
}

时间复杂度是n的平方，空间复杂度也是n的平方

这也是个二维动态规划，这种情况下最好画出矩阵图，然后从矩阵中寻找dp数组的求解规律

Manacher算法

在思考的过程中，或许已经注意到回文的是对称的，则对称就涉及到奇偶性的对称轴，则我们可以想办法将字符串无论奇偶统一为奇数或者偶数。

方法是在字符首位和之间添加特殊字符(即不会在原字符串中出现的字符)，使字符串统一变为奇数。

如字符串aba，添加#字符变为#a#b#a#
字符串abba，添加#字符变为#a#b#b#a#

我们把一个回文串中最左或最右位置的字符与其对称轴的距离称为回文半径。对于已经预处理好的字符串我们用数组rl[i]来记录以字符S[i]为中心的最长回文子串向左/右扩张的长度(注意包括S[i])。我们一般对字符串从左往右处理，因此这里定义RL[i]为第i个字符为对称轴的回文串的最右一个字符与字符i的距离。对于上面插入分隔符之后的两个串，可以得到RL数组：

1
2
3
4
5
6
7
8
9
char:    # a # b # a #
 RL :    1 2 1 4 1 2 1
RL-1:    0 1 0 3 0 1 0
  i :    0 1 2 3 4 5 6

char:    # a # b # b # a #
 RL :    1 2 1 2 5 2 1 2 1
RL-1:    0 1 0 1 4 1 0 1 0
  i :    0 1 2 3 4 5 6 7 8

上面我们还求了一下RL[i]-1。通过观察可以发现，RL[i]-1的值，正是在原本那个没有插入过分隔符的串中，以位置char[i]为对称轴的最长回文串的长度。那么只要我们求出了RL数组，就能得到最长回文子串的长度。

于是问题变成了，怎样高效地求的RL数组。基本思路是利用回文串的对称性，扩展回文串。

我们再引入一个辅助变量MaxRight，表示当前访问到的所有回文子串，所能触及的最右一个字符的位置。另外还要记录下MaxRight对应的回文串的对称轴所在的位置，记为pos，它们的位置关系如下。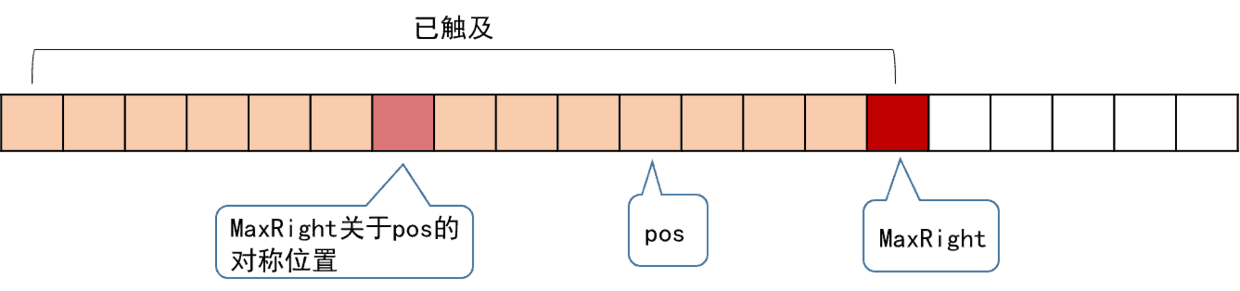

我们从左往右地访问字符串来求RL，假设当前访问到的位置为i，即要求RL[i]，在对应上图，i必然是在pos右边的。但我们更关注的是，i是在MaxRight的左边还是右边。我们分情况来讨论。

1、i在MaxRight左边
i在左边右分为两种情况，

  • 第一种情况用图表示如下

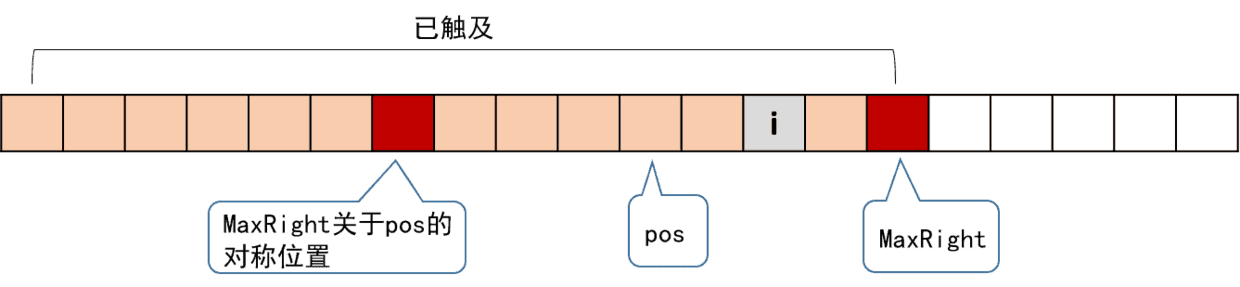
我们知道，图中两个红色块之间（包括红色块）的串是回文。并且以i为对称轴的回文串，是与红色块间的回文串有所重叠的。我们找到i关于pos的对称位置j，这个j对应的RL[j]我们是已经算过的。根据回文串的对称性，以i为对称轴的回文串和以j为对称轴的回文串，有一部分是相同的。这里又有两种细分的情况。

  • 以j为对称轴的回文串比较短，短到像下图这样(即rl[j] <= maxRigth - i)。

    这时我们知道RL[i]至少不会小于RL[j]，并且已经知道了部分的以i为中心的回文串，于是可以令RL[i]=RL[j]。但是以i为对称轴的回文串可能实际上更长，因此我们试着以i为对称轴，继续往左右两边扩展，直到左右两边字符不同，或者到达边界。
    或者看这个图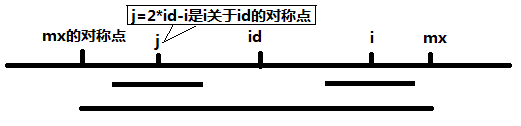

    当mx – i >= rl[j], 这时候以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于i和j对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以P[i]至少等于p[j], 后面的再继续匹配。

注：上图中其实rl[i]一定等于rl[j],后面不用再匹配了。因为如果rl[i]后面还可以继续匹配，根据对称性，rl[j]也可以继续扩展了

  • 以j为对称轴的回文串很长，像下图(即rl[j] > maxRigth - i)：

    这时，我们只能确定，两条蓝线之间的部分（即不超过MaxRight的部分）是回文的，于是从这个长度开始，尝试以i为中心向左右两边扩展，，直到左右两边字符不同，或者到达边界。
    或者看这个图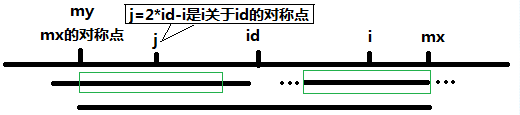

    当mx – i < rl[j]，以S[j]为中心的回文子串不完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，上图中两个绿框所包围的部分是相同的，也就是说以S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说rl[i] 至少等于 mx - i，至于mx之后的部分是否对称，就只能老老实实去匹配了。

当i在MaxRight左边时，主要是求chars[i]向右查找回文的初始步长是多少，其实完全可以无论i落在何处，直接将rl[i]初始化为1，然后向右查找。这样分情况讨论只是以免重复计算。

不论以上哪种情况，之后都要尝试更新MaxRight和pos，因为有可能得到更大的MaxRight。

具体操作如下：

1
2
3
step 1: 令RL[i]=min(RL[2*pos-i], MaxRight-i)
step 2: 以i为中心扩展回文串，直到左右两边字符不同，或者到达边界。
step 3: 更新MaxRight和pos

2、当i在MaxRight的右边

遇到这种情况，说明以i为对称轴的回文串还没有任何一个部分被访问过，于是只能从i的左右两边开始尝试扩展了，当左右两边字符不同，或者到达字符串边界时停止。然后更新MaxRight和pos。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
public static String proString(String s){
    StringBuffer stringBuffer = new StringBuffer();
    for (int i=0; i<s.length(); i++){
        stringBuffer.append("#").append(s.substring(i, i+1));
    }
    return stringBuffer.append("#").toString();
}
public static String manacher(String s){
    String proStr = proString(s);
    char[] chars = proStr.toCharArray();
    int[] rl = new int[chars.length];

    int pos = 0;
    int maxRight = 0;
    rl[0] = 1;
    for (int i=1; i<chars.length; i++){
    	// 分情况对rl[i]赋初始值
        if (i > maxRight){
            rl[i] = 1;
        }else {
            // 2*pos-1 是 pos - (pos - i)
            rl[i] = Math.min(rl[2 * pos - i], maxRight - i);
        }
        while ((i - rl[i] >= 0) && (i + rl[i] < chars.length) ){
            if (chars[i+rl[i]] == chars[i-rl[i]]){
                if (rl[i] >= maxRight){
                    maxRight = i + rl[i];
                    pos = i;
                }
                rl[i]++;
            }else {
                break;
            }
        }
    }
    int longest = 0;
    int start = 0;
    // 从rl中找出最大的半径
    for (int i=0; i<rl.length; i++){
        if (rl[i] > longest ){
            longest = rl[i] - 1;
            start = i;
        }
    }
    StringBuffer stringBuffer = new StringBuffer();
    // 从start为中心，分别向左向右拼字符串
    for (int i=longest; i>0; i--){
        stringBuffer.append(chars[start-i]);
    }
    for (int i=0; i<longest; i++){
        stringBuffer.append(chars[start + i]);
    }
    return stringBuffer.toString().replace("#","");
}

此算法中解决奇偶的方法值得借鉴。

参考

最长回文子串——Manacher 算法
LeetCode:Longest Palindromic Substring 最长回文子串