MapReduce源码解析--TotalOrderPartitioner

MR本身就具有排序功能，但是其分布式的特性使其无法较理想的进行全局排序。难道要想使用MR进行全局排序时只能将其结果都输入到一个reduce中？那这不就违背了其分布式的特性了嘛。于是大牛们想到了在map分区时保证分区的有序性，使其分配到第一个reduce中的key一定小于分配到第二个reduce中的key，此功能就是本篇要解析的分区类TotalOrderPartitioner。

上篇从应用的角度展示了TotalOrderPartitioner如何进行全局排序。本篇从代码的角度解析下TotalOrderPartitioner是怎么实现的，其中又用到了哪些黑科技。。。

TotalOrderPartitioner之所以能够实现全局排序，是因为其在分区时依赖一个分区文件，其文件中记录了将key进行分区的分界点，是这些分界点起到了关键作用。这些分界点保证了某一区间的key分到同一个reduce中，而TotalOrderPartitioner只是将key和分界点比较的过程进行了优化，使其在大数据规模下能够高效的进行。

TotalOrderPartitioner实现高速查询架构

TotalOrderPartitioner对不同Key的数据类型提供了两种方案：

对于只能WritableComparable而不能BinaryComparable类型的key，也可以理解成数值类型的数据(如IntWritable，在实现时只实现了WritableComparable接口)，TotalOrderPartitioner采用二分查找来确定当前key所在的reduce index。其二分查找是通过调用Arrays.binarySearch实现的。其时间复杂度是O(log(reduce num))。
对于可以BinaryComparable的key，也可以理解为字符串类型数据(如Text，BytesWritable，在实现时继承了BinaryComparable父类)，则构建一个Trie树，使字符串按照字典序进行排序。Trie树的查找时间复杂度是O(d)，d为树的深度(根的深度为1)，空间复杂度是O(255^(d-1))。

TotalOrderPartitioner源码解析

TotalOrderPartitioner实现了Configurable接口，在setConf中进行初始化，代码如下：

public void setConf(Configuration conf) {
    try {
        this.conf = conf;
        String parts = getPartitionFile(conf);
        final Path partFile = new Path(parts);
        final FileSystem fs = (DEFAULT_PATH.equals(parts))
                ? FileSystem.getLocal(conf)     // assume in DistributedCache
                : partFile.getFileSystem(conf);

        Job job = new Job(conf);
        // 得到map output key的类型，
        // 将partition file中key读取为keyClass类型
        Class<K> keyClass = (Class<K>)job.getMapOutputKeyClass();
        // 读取partition file，此文件为sequenceFile
        K[] splitPoints = readPartitions(fs, partFile, keyClass, conf);
        if (splitPoints.length != job.getNumReduceTasks() - 1) {
            throw new IOException("Wrong number of partitions in keyset");
        }
        // 得到job中设置的比较器，
        // 此比较器用在判断partition file中key是否按照升序排列，
        // 其次是在二分查找中用，
        RawComparator<K> comparator =
                (RawComparator<K>) job.getSortComparator();
        // 判断key是否升序
        for (int i = 0; i < splitPoints.length - 1; ++i) {
            if (comparator.compare(splitPoints[i], splitPoints[i+1]) >= 0) {
                throw new IOException("Split points are out of order");
            }
        }
        boolean natOrder =
                conf.getBoolean(NATURAL_ORDER, true);
        // 可BinaryComparable并且按照字典序比较则构建Trie树进行查找
        // 否则使用二分查找
        if (natOrder && BinaryComparable.class.isAssignableFrom(keyClass)) {
            partitions = buildTrie((BinaryComparable[])splitPoints, 0,
                    splitPoints.length, new byte[0],
                    // Now that blocks of identical splitless trie nodes are
                    // represented reentrantly, and we develop a leaf for any trie
                    // node with only one split point, the only reason for a depth
                    // limit is to refute stack overflow or bloat in the pathological
                    // case where the split points are long and mostly look like bytes
                    // iii...iixii...iii   .  Therefore, we make the default depth
                    // limit large but not huge.
                    conf.getInt(MAX_TRIE_DEPTH, 200));
        } else {
            partitions = new BinarySearchNode(splitPoints, comparator);
        }
    } catch (IOException e) {
        throw new IllegalArgumentException("Can't read partitions file", e);
    }
}

TotalOrderPartitioner构建成功用于查找的数据结构之后，在map中调用getPartition就ok了，代码如下：

1
2
3

public int getPartition(K key, V value, int numPartitions) {
    return partitions.findPartition(key);
}

通过getPartition这个入口，可以根据key在不同的数据结构中快速查找。下面就来看下两种数据结构是如何实现的。先看较简单的二分查找。

二分查找

partitions是Node类型的，在setConf中通过构造一个BinarySearchNode来对其赋值，由此可见BinarySearchNode肯定实现了Node接口。BinarySearchNode比较简单，在此贴了全部代码：

class BinarySearchNode implements Node<K> {
    private final K[] splitPoints;
    private final RawComparator<K> comparator;
    BinarySearchNode(K[] splitPoints, RawComparator<K> comparator) {
        this.splitPoints = splitPoints;
        this.comparator = comparator;
    }
    public int findPartition(K key) {
        final int pos = Arrays.binarySearch(splitPoints, key, comparator1) + 1;
        return (pos < 0) ? -pos : pos;
    }
}

其构造方法将分界点数组和比较器传入，然后在findPartition中调用Arrays.binarySearch对目标key进行查找。则查找逻辑主要在Arrays.binarySearch中实现，我们看下其源码实现：

private static <T> int binarySearch0(T[] a, int fromIndex, int toIndex,
                                     T key, Comparator<? super T> c) {
    // 比较器c为null，则使用Arrays的默认比较器
    if (c == null) {
        return binarySearch0(a, fromIndex, toIndex, key);
    }
    int low = fromIndex;
    int high = toIndex - 1;

    while (low <= high) {
        int mid = (low + high) >>> 1;
        T midVal = a[mid];
        int cmp = c.compare(midVal, key);
        if (cmp < 0)
            low = mid + 1;
        else if (cmp > 0)
            high = mid - 1;
        else
            return mid; // key found
    }
    return -(low + 1);  // key not found.
}

这是jdk的默认实现，需要注意的是未找到目标key时返回-(low+1)，其中low是该元素要插入的位置，也就是low索引之前的元素都比目标key要小，但是之所以返回-(low+1)而不是-low，是因为假如目标key比所有的元素都小时，那么最后一次比较是停留在index=0的位置，这时候low=0,那么我们返回给调用者的值就是0了，而不是一个负数，这样我们拿到0并不知道他是没匹配到，还是该元素就在第一个元素。所以我们要保证如果找不到就返回一个负数。所以就多减个1 这样-1就表示没找到并且该元素必须插到0的位置上。

对于可以进行数值比较的key使用二分查找比较简单高效，但对于字符类型的key比较时可以使用更高效的Trie树比较。下面看下Trie树。

Trie树

Trie树又称字典树、前缀树，是一种有序树。跟HashMap的功能相似，都是key-value映射，只不过Trie常用于有公共前缀的字符串映射，并且key只能是字符串。
Trie树的查询效率较高，时间复杂度为O(n)，n为字符串的长度也可以理解成Trie树的深度，与Trie树中保存的字符串个数无关。只是其空间复杂度较大，是一个典型的拿空间换时间的数据结构。

Trie树的基本性质如下：

根节点不包含字符，除根节点之外所有的节点最多包含一个字符(不是一个字符串)。
把根节点到某一节点的路径上的字符连接起来就是该节点对应的字符串。
每个节点的所有子节点包含的字符都不相同，并且每个节点的所有子节点都有相同的前缀。
如果字符的种类是n，则每个节点不管其子节点上是否有对应的value都会有n个子节点。(这就浪费了很多空间)
插入和查找的复杂度是O(n)，n为字符串的长度。

在对TotalOrderPartition中Trie树的构造过程进行解析之前，先对其中相关的内部类进行下介绍。

Node是一个接口，TrieNode是抽象类，扩展了Node接口(BinarySearchNode实现了Node接口，作为数值型数据比较节点)，作为Trie树中抽象出的节点类。

interface Node<T> {
// 所有方法的访问权限自动被声明为public。
// 确切的说只能为public，当然你可以显示的声明为protected、private，但是编译会出错
// 接口中可以定义"成员变量"，或者说是不可变的常量，
// 因为接口中的"成员变量"会自动变为public static final
    int findPartition(T key);
}

// 抽象类实现接口时，不用必须实现接口中的方法
// TrieNode 并没有实现Node接口中的findPartition方法
static abstract class TrieNode implements Node<BinaryComparable> {
    private final int level;
    TrieNode(int level) {
        this.level = level;
    }
    int getLevel() {
        return level;
    }
}

接口和抽象类介绍完就剩下Trie树中标识各个节点状态的对象类了，包括InnerTrieNode(有key的节点)、UnsplitTrieNode()、SinglySplitTrieNode(单个切分节点，存放value值的节点)和LeafTrieNode()。

对Trie树有了初步的了解，下面看下Trie树的构造过程。TotalOrderPartition中Trie树的构造是类似深度遍历那样递归的对树进行构建。

在构建过程中需要注意几点：

Trie树中节点分两种情况，一种是不存放字符的节点，一种是存放字符的情况。对于不存放字符的节点不用为其构建子树，对于本例中的情况，由于此节点不存放字符也就不用切分，则这类情况的节点的状态是UnsplitTrieNode。对于存放字符的节点则根据是否是叶子节点又分为InnerTrieNode(根节点也是InnerTrieNode)和SinglySplitTrieNode。
由于本例中比较的是字符，则每个节点最多有256(ascii码0-255表示字符)个子树，从左到右依次0-255，每个字符存放在对应ascii码的子树上，如字符1的ascii码是49，则存放在标号为49的子树上。
partition file中的key是按照升序排好的，_相邻的字符会有部分前缀相同，则无需分别对单个key中的字符进行构建，而是每次对所有key的第i个字符进行构建_，用currentBound标识是对第几个key中的字符进行构建。

构建代码入口如下：

// 参数为 splitPoints, 0, splitPoints.length, new byte[0], conf.getInt(MAX_TRIE_DEPTH, 200)
private TrieNode buildTrieRec(BinaryComparable[] splits, int lower,
                              int upper, byte[] prefix, int maxDepth, CarriedTrieNodeRef ref) {
    // 可见代码中树的深度不包括根节点
    // 前缀数组标识了当前Trie树的深度
    final int depth = prefix.length;
    // We generate leaves for a single split point as well as for
    // no split points.
    // 为单个切分点生成叶子节点，就像为那些无法切分点生成叶子节点一样
    // 当前节点只有一个子节点有值时，不用循环设置子节点的状态，直接将此节点变为叶子节点
    // 当前节点有几个子节点有值，是由upper-lower来标识的
    // 叶子节点包括 UnsplitTrieNode、SinglySplitTrieNode和LeafTrieNode
    if (depth >= maxDepth || lower >= upper - 1) {
        // If we have two consecutive requests for an unsplit trie node, we
        // can deliver the same one the second time.
        if (lower == upper && ref.content != null) {
            return ref.content;
        }
        TrieNode  result = LeafTrieNodeFactory(depth, splits, lower, upper);
        // 为 ref.content 重新赋值
        ref.content = lower == upper ? result : null;
        return result;
    }
    // 有数值的节点声明为InnerTrieNode
    InnerTrieNode result = new InnerTrieNode(depth);
    // 实验数组
    byte[] trial = Arrays.copyOf(prefix, prefix.length + 1);
    // append an extra byte on to the prefix
    int currentBound = lower;
    // 0xFF为int的255，是byte类型的-1
    // 为当前节点生成0-254子节点的状态
    for(int ch = 0; ch < 0xFF; ++ch) {
        trial[depth] = (byte) (ch + 1);
        lower = currentBound;
        while (currentBound < upper) {
        	// 对第currentBound个key第trial.length个字符进行比较
        	// 当splits[currentBound]大时，当前节点无字符，跳出while循环，
        	// 将此节点变为UnsplitTrieNode状态
        	// 当splits[currentBound]小时，比较splits中下一个key的第trial.length字符
            if (splits[currentBound].compareTo(trial, 0, trial.length) >= 0) {
                break;
            }
            currentBound += 1;
        }
        // 存储当前字符所在的节点索引
        trial[depth] = (byte) ch;
        // 递归的对其节点构建子节点
        result.child[0xFF & ch]
                = buildTrieRec(splits, lower, currentBound, trial, maxDepth, ref);
    }
    // pick up the rest
    // 重置最后一层的值，便于构造第255个节点的值
    // for循环只是对0-254进行构建
    trial[depth] = (byte)0xFF;
    result.child[0xFF]
            = buildTrieRec(splits, lower, currentBound, trial, maxDepth, ref);

    return result;
}

首次buildTrieRec是通过buildTrie，传入的参数是存放key的数组splitPoints、开始索引lower为0、结束索引upper为splitPoints.length、prefix前缀数组byte[0]和最大深度默认是200。其中开始索引和结束索引是指splitPoints中第i个字符比当前子树节点的标号小的那些key的索引值，开始索引是指小于此标号的第一个key的索引，结束索引是指小于此标号的最后一个key的索引。

首次调用buildTrieRec时，如果splitPoints的长度大于2，则创建一个根节点，根节点的状态是InnerTrieNode，但是不存放任何字符。根节点创建之后由一个for循环为其254个子树创建节点的状态，第255个子树作为边界值在for循环之外进行创建。在构建子树时是按照深度优先遍历的方式进行构建，而子树的构建是由字符比较所决定的，对不同深度的子树比较的字符也不一样，则需要记录子树的深度和此时比较的字符，又由于Trie树是一层一个字符，则将当前比较字符及其前缀字符保存到数组，这样数组的长度就是子树的深度，数组中的元素值就是所需比较的字符。上面的代码中则是在for循环之前将前缀数组复制到trial数组(实验数组)中，将lower做为字符比较的第一个key，将其赋值给currentBound，由currentBound来标识比较的是当前集合中的第几个key。

每个节点有256个子树，从0开始标号，将第255个子树作为边界单独处理，则在for循环中对0-254子树进行处理(for(int ch=0; ch<0xFF; ch++))，由currentBound决定比较的是第几个key，由trial数组的长度决定比较key中的第几个字符，trial数组中的最后一个变量是ch，在for中的while循环里通过比较key的第trial.length个字符与ch的大小，找到这个字符在子树中的合适位置，并通过currentBound的值来统计当前key的集合中有多少个key中第trial.length个字符可以放在此子树上。然后对该节点进行递归的创建子树节点。
随后跳出for循环，设置trial的值，0xFF(byte类型为数值-1)，然后对255节点进行构建

用lowe和upper的值来判断build的逻辑，是创建子树或者Unsplit或者SinglySplit。build逻辑如下：

当lower和upper的差值小于等于1时，则进行是构建Unsplit(upper-lower==0)还是SinglySplit(upper-lower==1)。
当大于1时，则利用for循环构建子树。

下面看下UnsplitTrieNode和SinglySplitTrieNode两个类。

private class UnsplitTrieNode extends TrieNode {
    final int result;

    UnsplitTrieNode(int level, int value) {
        super(level);
        this.result = value;
    }
    // 返回该节点上的key被分配到的reduce id
    public int findPartition(BinaryComparable key) {
        return result;
    }
}

UnsplitTrieNode中result属性记录了该分支上的key应该被分配到哪个分区。

private class SinglySplitTrieNode extends TrieNode {
    final int               lower;
    final BinaryComparable  mySplitPoint;

    SinglySplitTrieNode(int level, BinaryComparable[] splitPoints, int lower) {
        super(level);
        this.lower = lower;
        this.mySplitPoint = splitPoints[lower];
    }
    // 这里决定了当key等于mySplitPoint时，会分配到下一个reduce中
    public int findPartition(BinaryComparable key) {
        return lower + (key.compareTo(mySplitPoint) < 0 ? 0 : 1);
    }
}

SinglySplitTrieNode中lower属性记录了当前key在key集合中的索引，属性mySplitPoint记录了分界点的值。

至此buildTrie的主要逻辑已分析完毕，接下来我们来个例子实践下。
切分节点为1983、1995、1999、2996，利用此4个切分节点构建Trie树如下图：

Trie树结构图

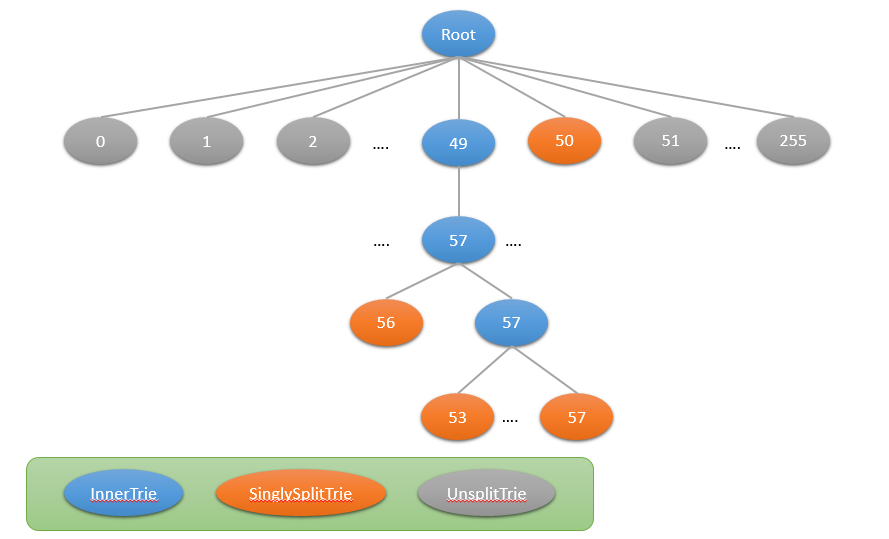
其中节点上的数字表示每个节点的标号，范围是0-255，也是每个字符的ascii码。

假如key为1973，则经过root->49->57，然后197比198小，则将其分配给reduce 0
假如key为1983，则经过root->49->57->56，将其分配给reduce 1
假如key为3，将其分配给reduce 3

NOTE

partition file中key是升序的，因为二分查找需要数据集是有序的和Trie树的构建需要数据是有序的
partition file中key的数据类型和map output key、reduce input key 相同
partition file中key的分布尽量均匀避免数据倾斜

彩蛋

Hadoop中提供的partition方法

HashPartitioner是mapreduce的默认partitioner。根据key的hash结果选择reduce。
BinaryPatitioner继承于Partitioner<BinaryComparable ,V>，是Partitioner的偏特化子类。该类提供leftOffset和rightOffset，在计算which reducer时仅对键值K的[rightOffset，leftOffset]这个区间取hash。
KeyFieldBasedPartitioner也是基于hash的个partitioner。KeyFieldBasedPartitioner可以灵活设置key中用于partition的字段，而不是把整个key都用来做partition。
TotalOrderPartitioner这个类可以实现输出的全排序。不同于以上3个partitioner，这个类并不是基于hash的。